맥북이 도착하고 난 뒤부터 코딩테스트를 시작하려 했지만, 맥북이 생각보다 늦게와서 (아니 한국에 들어왔는데 왜 배송이 안되냐고..ㅠㅠ) 데스크탑으로 공부를 시작했다!
앞에 문제들은 이미 풀어져 있길래,, 2588번부터 하나하나 단계별 풀어보기를 진행할 예정이다.
오늘은! 그 대망의 첫 번째 문제인 백준 2588 A*B를 풀 것이다.
오늘의 문제
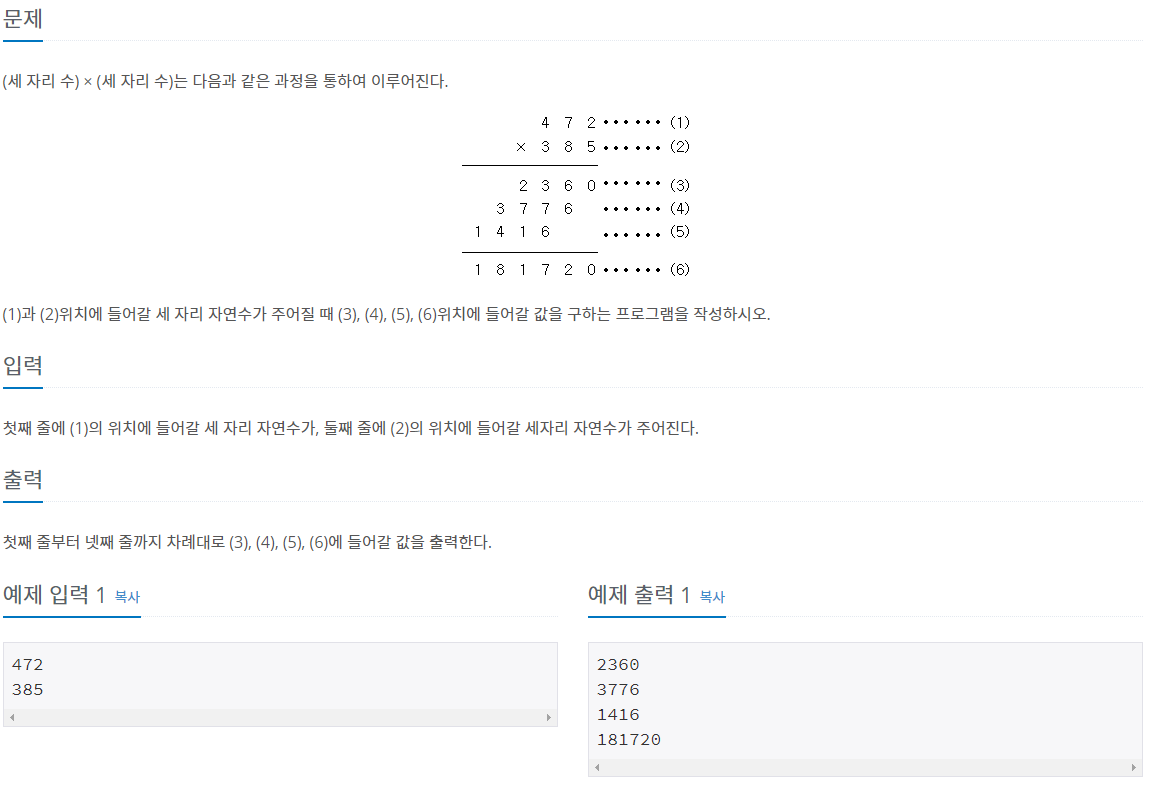
2588번의 문제는 두 정수 A*B를 계산할 때, 계산 과정을 모두 출력하는 것이다.
이 문제를 딱 봤을 때, 정해야 할것 하나와 알아야 할 것이 두 가지가 있는 것을 알 수 있다.
정해야 할것
1. 두 정수 중 어떤 것을 베이스로 할것인가?
알야아 할것
1. 곱해지는 수는 몇자리 수 인가? (365=3자리 수)
2. 곱해지는 수의 각 자리의 값은 무엇인가? (일의 자리, 십의 자리, 백의 자리 ...)
정해야 할 것은 그냥 첫 번째 수를 베이스로 했고, 따라서 두번 째 수는 자연스럽게 곱해지는 수로 정했다.
해당 문제는 수학적 지식만 조금 있다면 바로 구할 수 있다. 나 같은 경우에는 위의 방법이 바로 떠올랐고, 이미 알고있는 방법이기 때문에 바로 문제를 풀 수 있었다. (세 번 실패한건 비밀... 첫 번째는 오타로인한 컴파일 에러.. 두 번째는 클래스 명이 Main이어야 한다는 것을 까먹고 있었고,, 따라서 틀렸다...)
1. 곱해지는 수는 몇자리 수 인가?
우선 곱해지는 수가 몇자리 수인지 알아야 한다. 우리에게 주어지는 곱의 값은 매번 달라질 것이고, 따라서 하드코딩을 통해 값을 매번 지정할 수 없기 때문이다.
예를 들어, 곱해지는 수가 한자리 수일때의 경우, 두자리 수일 때의 경우, 세자리 수일 때의 경우, ... 엄청 큰 자리수일 때의 경우 를 모두 코딩할수는 없잖아!
해당 질문은 log를 통해 쉽게 구할 수 있다. 먼저 자리수에 대해 우리가 표현할 때, 1의 자리는 다음과 같이 표현할 수 있다.
$$ n * 10^0 $$
마찬가지로 10의 자리는 다음과 같이 표현할 수 있다.
$$ n * 10^1 $$
이쯤 되면 내가 무엇을 하고자 하는지 이해 할 수 있다! 즉, 우리는 정수의 자리수를 표현하기 위해 다음과 같이 일반화 할 수 있다.
$$ n * 10^m ( m >= 0, integer ) $$
이 때, n은 우리가 표현하고자 하는 수 이고, m은 해당 숫자의 자릿수 이다.
우리는 지수를 로그로 표현할 수 있는 것을 고등학교 수학에서 배웠다.
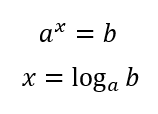
즉, 자리수를 로그를 통해 표현할 수 있는 것인데, 위의 일반화를 로그로 표현해 보면 다음과 같이 될 수 있다.
$$ m = log_10 n $$
이 때, m은 자리수가 되고, n은 표헌하고자 하는 수 이다! 그런데, log에서는 한가지 주의할 점이 있는데, log 0이 정의되지 않는 점이다.
$$ 10^m = 0 $$ log 0을 지수로 나타내었을 때 위와 같은 식이되고, 해당 식을 만족하는 m의 값은 없기 때문이다.
따라서, 우리가 구하고자 하는 자릿수는 최종적으로 다음과 같은 식이 된다.
$$ m = {log_{10} n} + 1$$
2. 곱해지는 수의 각 자리의 값은 무엇인가? (일,십,백, ...의 자리)
이제 해당하는 m 자리의 값이 무엇인지 구하면 된다.
해당 질문은 놀랍게도 몫을 구하는 식으로 쉽게 풀 수 있다. 위에서 우리는 모든 수를 다음과 같이 표현할 수 있다는 걸 이미 인지했다.
$$ n = 10^m $$
우리는 궁극적으로 n이 무엇인지 구해야 한다. 수는 0~9까지 중 하나로 표현할 수 있고, 거기에 자릿수를 곱해주게 되면, n이 무엇인지 알 수 있다.
"그래서 도대체 0~9 중 무엇인지 어떻게 아는데?!"
우리가 어떤 수를 나눌 때, 해당 식은 다음과 같이 표현된다.
$$ N = Qx + R $$
아직도 감이 안오는가?!?!
우리가 구하고자 하는 수 N에 대하여 Q=10(몫의 밑)이고, x(몫의 배수)가 얼마든 간에 R의 범위는 0~9로 한정된다.
이 때 우리는 몫의 배수를 자리수로 해 줄 것이다. 무슨 말이냐면, 다음과 같이 나타낼 수 있다.
$$ 10^m % 10 $$
여기서 문제점은, 우리가 아무리 10 % 10, 100 % 10, 10....0, % 10을 해도 0이 나온다는 점이다. 그 이유는, 우리 본래 수를 아직 구하지 않았기 때문인데, 본래 우리가 찾고자 하는 수는 다음과 같이 구할 수 있다. 예를 들어, 385에 대하여 8을 구하고자 할 때는 다음과 같다.
$$ {385 / 10^1} % 10 = 8.5 $$
이 때, 우리가 사용하는 수는 정수이기 때문에, 8로 구해지는 것을 알 수 있다.
이제 위 두 수식을 근거로 코드를 작성해보자!
문제의 풀이 과정을 출력하기 위한 함수 하나, 그리고 메인함수 하나 하여 총 두 개의 함수를 만들 것이다.
메인 함수는 두 수를 입력받고, 풀이 과정을 출력하는 함수를 호출하며 최종적으로 두 식의 연산 결과를 출력할 것이다.
BufferedReader와 InputStreamReader를 이용하여 입력받을 수 있지만, 간단한 문제이고 메모리, 속도제한 등 아무 것도 없기 때문에 java.util.Scanner를 이용하여 두 수를 입력받을 것이다.
따라서 최종 코드는 다음과 같다.
public class Number2588{
public static void main(String args[]){
try(Scanner scan = new Scanner(System.in)){
int a = scan.nextInt();
int b = scan.nextInt();
printNth(a, b);
System.out.println(a*b);
}
}
public static void printNth(int a, int b){
int length = (int)(Math.log10(b)+1);
for(int i = 0; i < length; i++){
int tempB = b / (int)Math.pow(10, i) % 10; // tempB 없이 바로 출력해도 된다.
System.out.println(a * tempB);
}
}
}
'공부 > 알고리즘' 카테고리의 다른 글
| [Java 코딩테스트] 백준 1110 문제풀이 / 더하기 사이클 (0) | 2021.07.22 |
|---|---|
| [Java 코딩테스트] 백준 2438 문제풀이 Dynamic Programming (0) | 2021.07.19 |
| [Java 코딩테스트] 백준 15552번 문제 풀이 (0) | 2021.07.18 |
| [Java 코딩테스트] 백준 2884번 문제풀이 (0) | 2021.07.18 |
| [Java 코딩테스트] 백준 2753번 문제풀이 (0) | 2021.07.13 |