Description
- 본 문제는 그리디로 풀 수 있다.
- 한 곡괭이로 캘 수 있는 5번 횟수에 대해 각 구간을 정한다.
- 모든 미네랄에 대해 곡괭이로 캘 수 있는 횟수까지 대해 구간을 정한다.
- 곡괭이 1개라면, 5회, 2개라면 10회, …
- 이 때 곡괭이로 캘 수 있는 수량 보다 미네랄이 적을 수 있으므로, 내가 볼 구간의 length는
- Math.min( 곡괭이 횟수, 광물 수 / 5 )
- / 5를 해주는 이유는 한 곡괭이로 5번 밖에 못 캐기 때문이다.
- Math.min( 곡괭이 횟수, 광물 수 / 5 )
- 이에 대해 모든 곡괭이를 사용하여 얼마만큼의 비용이 발생하는지 확인한다.
- 곡괭이가 없어도 일단 계산한다. 나중에 조건을 이용해 사용하지 않으면 되기 때문
- 모든 미네랄에 대해 곡괭이로 캘 수 있는 횟수까지 대해 구간을 정한다.
- 각 구간에 대해 값을 모두 구했다면, 이를 돌 곡괭이 > 철 곡괭이 > 다이아몬드 곡괭이 순으로 우선순위 큐에 삽입한다.
- 돌 곡괭이로 많은 비용이 발생했다면, 이는 광물이 비싸다는 뜻이고, 따라서 더 좋은 곡괭이로 캘 수록 효율이 높아지기 때문.
- 철 곡괭이도 마찬가지
- 이 후 우선순위 큐 에서 하나씩 꺼내면서 가지고 있는 제일 좋은 곡괭이로 캤을 때 발생하는 비용을 추가하면 정답
- 이 때 이미 비용은 계산해 놓았기 때문에, 해당 구간에서 해당 곡괭이 값을 찾으면 된다.
Result
import java.util.*;
class Solution {
public int solution(int[] picks, String[] minerals) {
int answer = 0;
int picksCount = 0;
PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> {
if(o2[2] != 0 || o1[2] != 0)
return o2[2] - o1[2];
if(o2[1] != 0 || o1[1] != 0)
return o2[1] - o1[1];
return o2[0] - o1[0];
});
for(int i = 0; i < picks.length; i++) picksCount += picks[i];
//* 좋은 곡괭이로 캘 수록 피로도는 적어진다.
//* 좋은 곡괭이로 좋은 광물을 캘 수록 피로도는 적다.
//* 다이아몬드가 많을 때 다이아로 캐는게 좋다.
//* 철이 많을 때 철로 캐는게 좋다.
//* 돌이 많을 때 돌로 캐는게 좋다.
//* 한 번에 5개씩 캐야 하니, 각 구간의 threshold를 구한다.
//* 각 구간에 대해 모든 곡괭이 값을 구하고 최소값으로 갱신
//* 필요한 tresh 칸 수 = 최대: 곡괭이 수, 최소: minerals.length / 5 + 1
//* 각 구간에 대한 곡괭이 사용 값
// int[][] thresh = new int[Math.min(picksCount, (minerals.length/5) + 1)][3];
int[] temp = { 0, 0, 0 };
for(int i = 0; i < minerals.length; i++){
if(i > 0 && i % 5 == 0){
pq.offer(new int[]{
temp[0], temp[1], temp[2]
});
temp[0] = 0;
temp[1] = 0;
temp[2] = 0;
}
if(i >= picksCount * 5) break;
switch(minerals[i]) {
case "diamond":
temp[0] += 1;
temp[1] += 5;
temp[2] += 25;
break;
case "iron":
temp[0] += 1;
temp[1] += 1;
temp[2] += 5;
break;
default:
temp[0] += 1;
temp[1] += 1;
temp[2] += 1;
break;
}
}
if(temp[0] != 0 || temp[1] != 0 || temp[2] != 0){
pq.offer(new int[]{
temp[0], temp[1], temp[2]
});
}
while(!pq.isEmpty()){
int[] current = pq.poll();
for(int i = 0; i < picks.length; i++){
if(picks[i] != 0){
answer += current[i];
picks[i]--;
break;
}
}
}
return answer;
}
}Problem
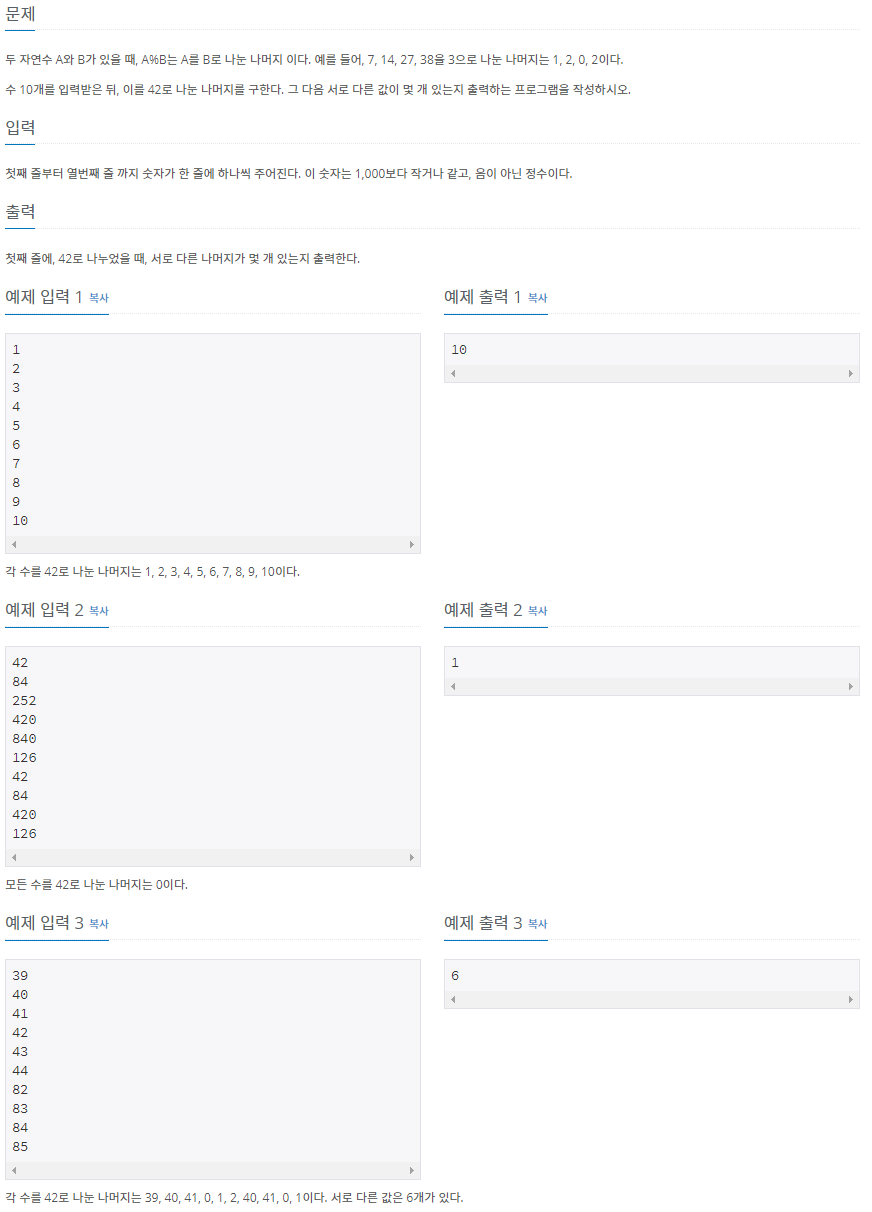
문제 설명
마인은 곡괭이로 광산에서 광석을 캐려고 합니다. 마인은 다이아몬드 곡괭이, 철 곡괭이, 돌 곡괭이를 각각 0개에서 5개까지 가지고 있으며, 곡괭이로 광물을 캘 때는 피로도가 소모됩니다. 각 곡괭이로 광물을 캘 때의 피로도는 아래 표와 같습니다.

예를 들어, 철 곡괭이는 다이아몬드를 캘 때 피로도 5가 소모되며, 철과 돌을 캘때는 피로도가 1씩 소모됩니다. 각 곡괭이는 종류에 상관없이 광물 5개를 캔 후에는 더 이상 사용할 수 없습니다.
마인은 다음과 같은 규칙을 지키면서 최소한의 피로도로 광물을 캐려고 합니다.
- 사용할 수 있는 곡괭이중 아무거나 하나를 선택해 광물을 캡니다.
- 한 번 사용하기 시작한 곡괭이는 사용할 수 없을 때까지 사용합니다.
- 광물은 주어진 순서대로만 캘 수 있습니다.
- 광산에 있는 모든 광물을 캐거나, 더 사용할 곡괭이가 없을 때까지 광물을 캡니다.
즉, 곡괭이를 하나 선택해서 광물 5개를 연속으로 캐고, 다음 곡괭이를 선택해서 광물 5개를 연속으로 캐는 과정을 반복하며, 더 사용할 곡괭이가 없거나 광산에 있는 모든 광물을 캘 때까지 과정을 반복하면 됩니다.
마인이 갖고 있는 곡괭이의 개수를 나타내는 정수 배열 picks와 광물들의 순서를 나타내는 문자열 배열 minerals가 매개변수로 주어질 때, 마인이 작업을 끝내기까지 필요한 최소한의 피로도를 return 하는 solution 함수를 완성해주세요.
제한사항
picks는 [dia, iron, stone]과 같은 구조로 이루어져 있습니다.- 0 ≤ dia, iron, stone ≤ 5
- dia는 다이아몬드 곡괭이의 수를 의미합니다.
- iron은 철 곡괭이의 수를 의미합니다.
- stone은 돌 곡괭이의 수를 의미합니다.
- 곡괭이는 최소 1개 이상 가지고 있습니다.
- 5 ≤
minerals의 길이 ≤ 50minerals는 다음 3개의 문자열로 이루어져 있으며 각각의 의미는 다음과 같습니다.- diamond : 다이아몬드
- iron : 철
- stone : 돌
입출력 예
| picks | minerals | result |
|---|---|---|
| [1, 3, 2] | ["diamond", "diamond", "diamond", "iron", "iron", "diamond", "iron", "stone"] | 12 |
| [0, 1, 1] | ["diamond", "diamond", "diamond", "diamond", "diamond", "iron", "iron", "iron", "iron", "iron", "diamond"] | 50 |
입출력 예 설명
입출력 예 #1
다이아몬드 곡괭이로 앞에 다섯 광물을 캐고 철 곡괭이로 남은 다이아몬드, 철, 돌을 1개씩 캐면 12(1 + 1 + 1 + 1+ 1 + 5 + 1 + 1)의 피로도로 캘 수 있으며 이때가 최소값입니다.
입출력 예 #2
철 곡괭이로 다이아몬드 5개를 캐고 돌 곡괭이고 철 5개를 캐면 50의 피로도로 캘 수 있으며, 이때가 최소값입니다.
'공부 > 알고리즘' 카테고리의 다른 글
| [Java 코딩테스트] 프로그래머스 연속 펄스 부분 수열의 합 풀이 / 연속 배열의 최대 합 (0) | 2023.03.02 |
|---|---|
| [알고리즘] BackTracking 기법, N Queen 예시/ 퇴각검색 기법 (0) | 2021.08.26 |
| [알고리즘] 동적 계획법 / Dynamic Programming (0) | 2021.08.23 |
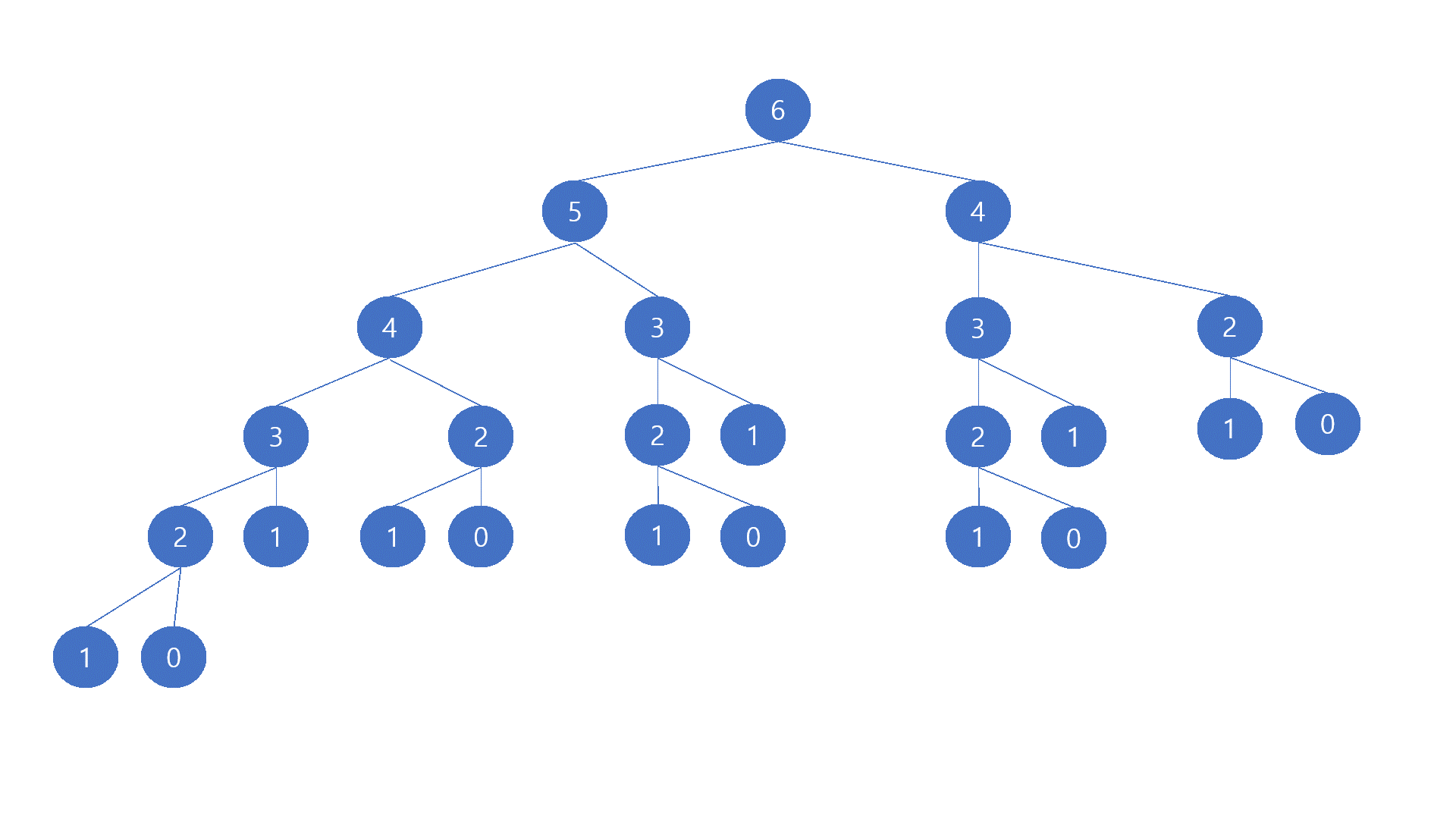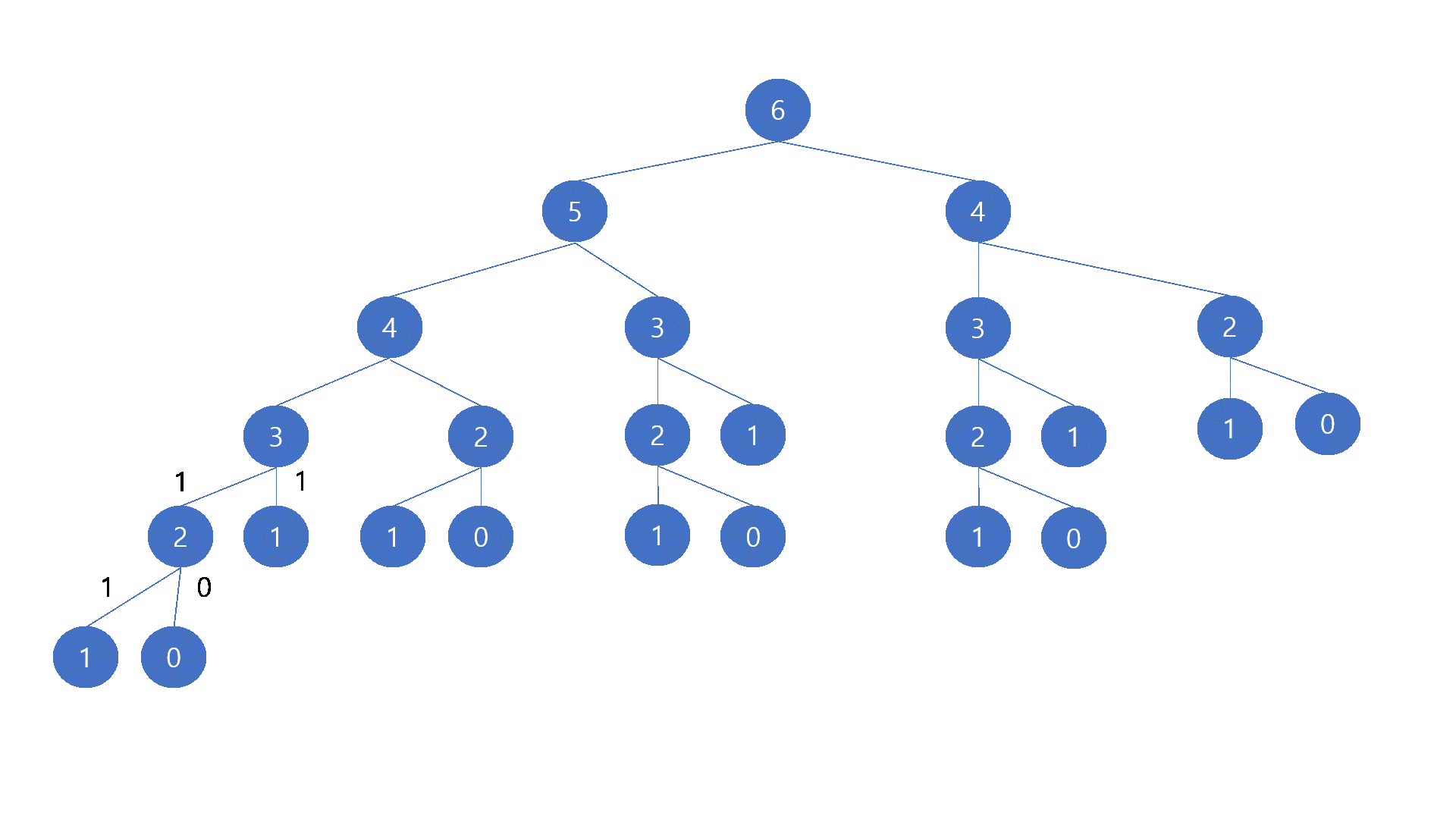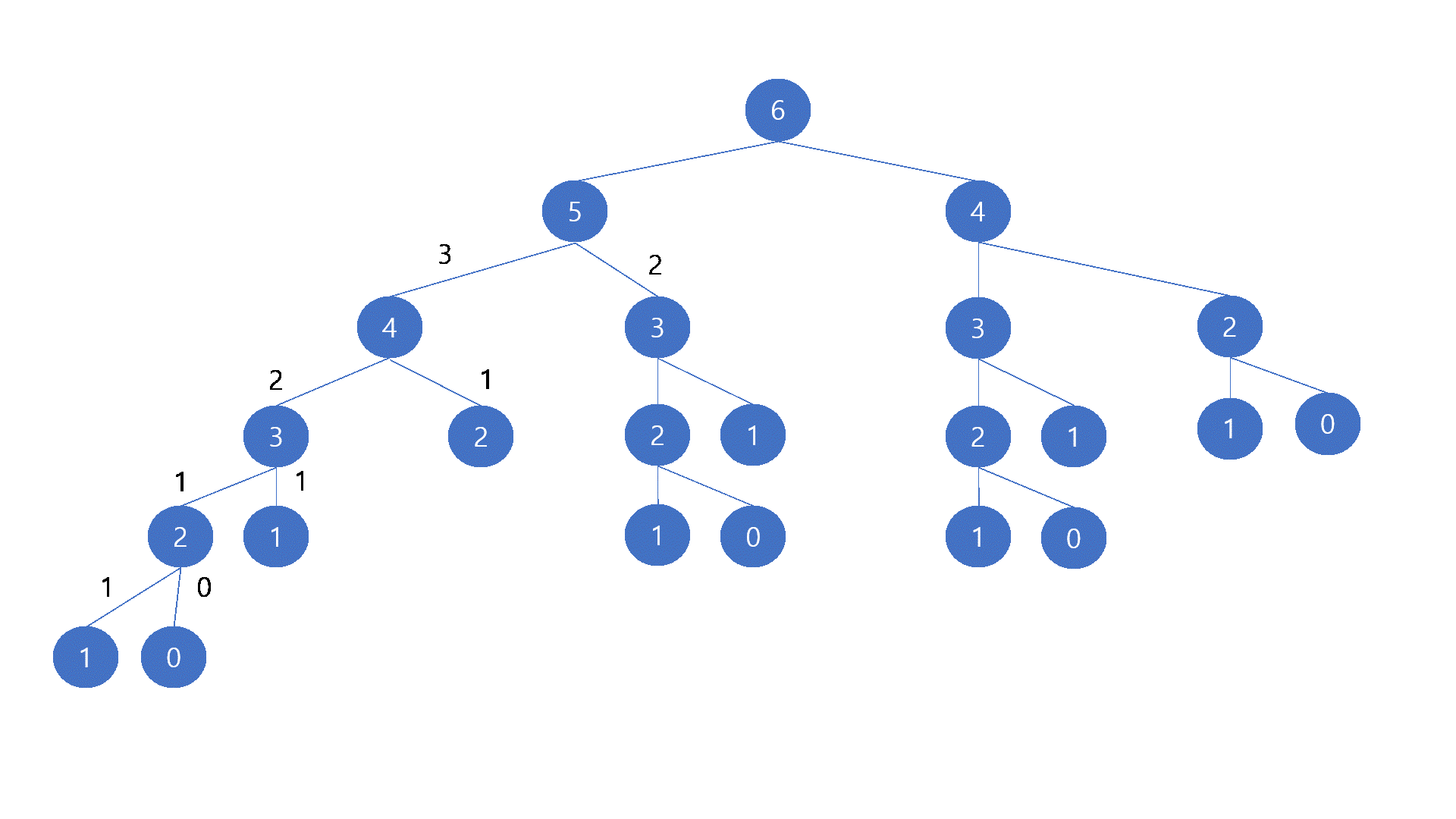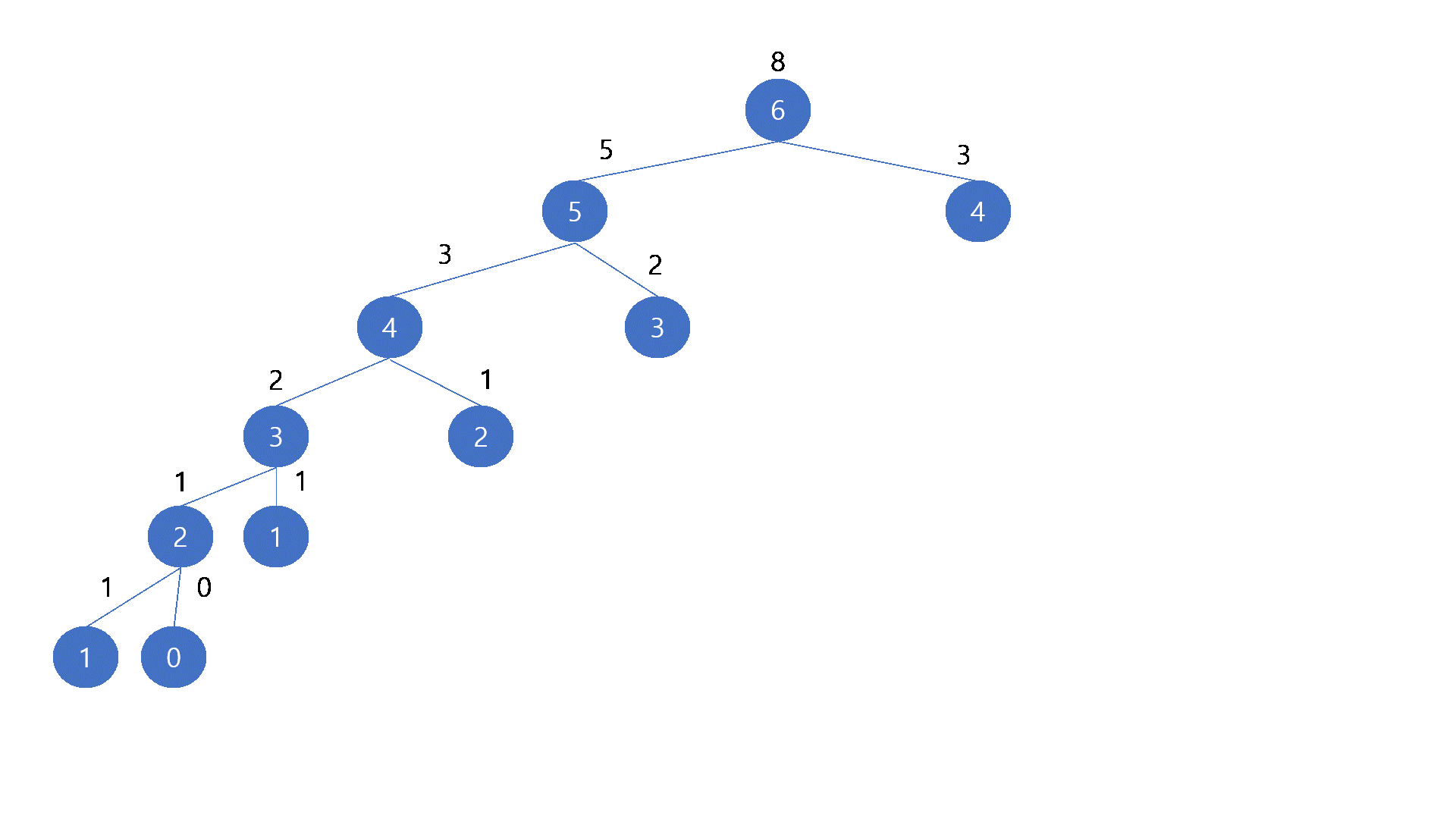
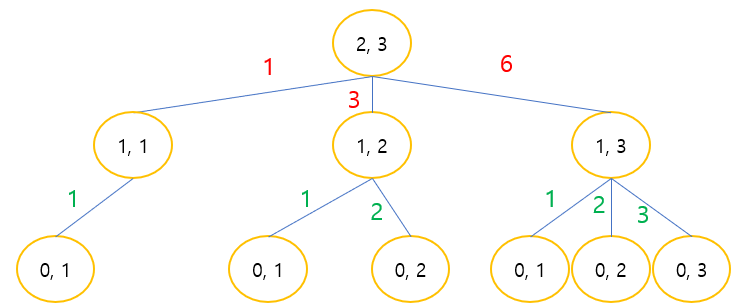
| [Java 코딩테스트] 백준 2775 부녀회장이 될테야 / Dynamic Programming (0) | 2021.08.18 |
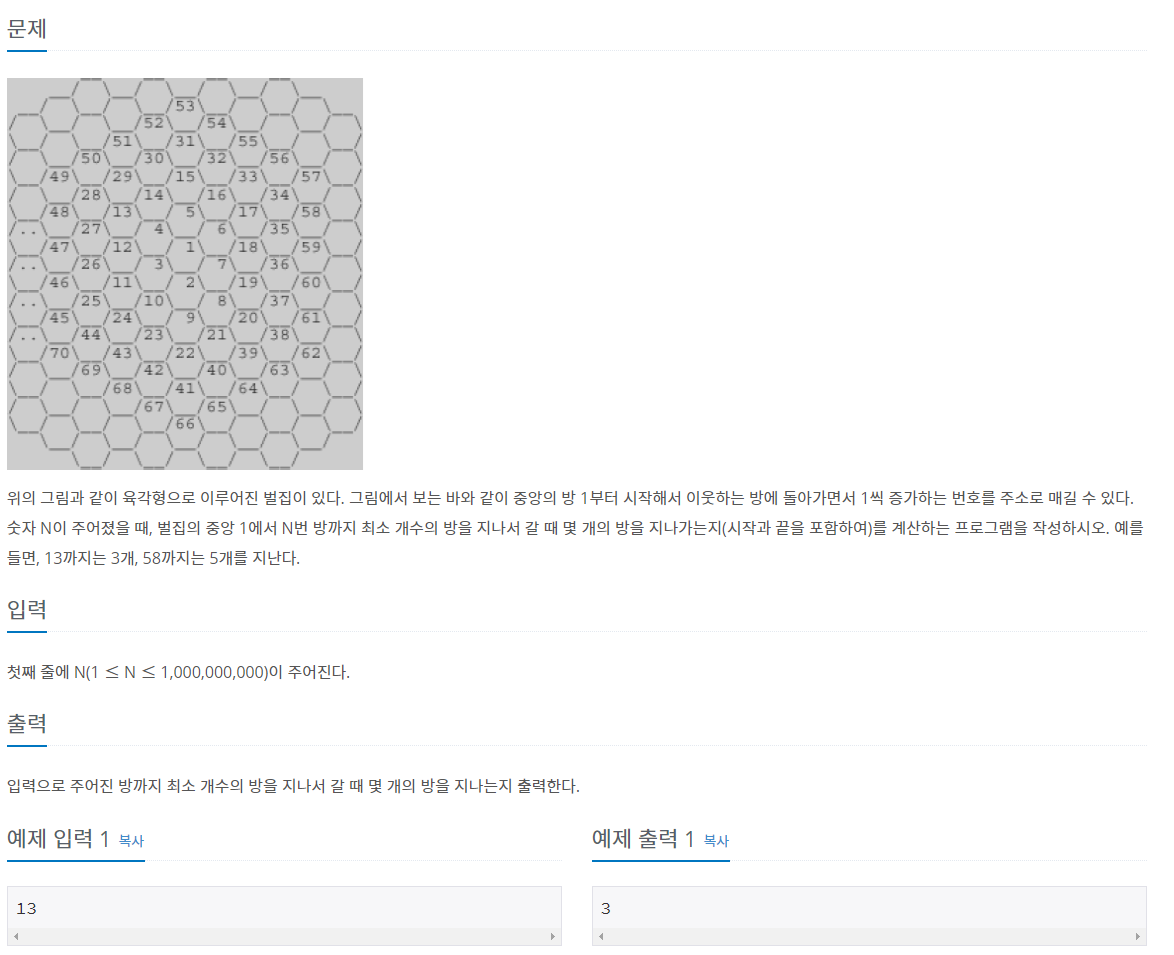
| [Java 코딩테스트] 백준 2292번 문제 풀이 / 백준 벌집 문제 (0) | 2021.08.10 |